| Varje år inträffar allvarliga och tragiska olyckor på de svenska
isarna i samband med isfiske eller skridskoåkning. I nästan alla fall hade dessa kunnat undvikas om iskunskaperna och omdömet varit bättre. Tyvärr så förolyckas många människor varje år just beroende på dåliga kunskaper,alkoholpåverkan och bristande omdöme. Med denna sida vill PIMPELFORUM bidraga till att minska dessa onödiga tragedier. När du läst detta och har ett gott omdöme vågar vi nästan utlova att du säkert kan gå ut på isarna när dessa bär. Men till sist är det trots allt ditt eget omdöme som avgör, är man t.ex. sjuk eller alkoholpåverkad så ger man sig inte ut! Vi önskar en nyttig och god läsning! |
Isens tillväxt beror på att värme leds bort ifrån isen. Isens undersida blir då kallare, och det vatten som är närmast under isen fryser. Ju större borttransporten är av värme, desto större blir isens tillväxthastghet. Borttransporten av värme beror på i huvudsak tre fenomen: utstrålning, värmeledning, ångbildning. I isprediktorn framgår det hur stor effekt respektive fenomen transporterar bort. Solen inverkar förstås negativt på istillväxten. Dessbättre lyser inte solen så länge på vintern och dessutom från en låg vinkel. Det gör att man i de flesta fall kan bortse från solens inverkan.
Enligt Stefan Boltzmanns lag strålar alla föremål värme, s.k. svartkroppstrålning. Denna strålning sker både till och från ett föremål, beroende på dess temperatur, omgivande temperatur och materialens fysiska egenskaper. Vid klart väder blir strålningen högre, eftersom den kan ske rakt ut i den kalla rymden. Det är p.g.a. denna egenskap som det blir mindre rimfrost på bilrutan när den står under carporten än om den står bredvid, trots att det är samma lufttemperatur.
Om isytan är varmare än omgivande luft, kommer värme att gå från den "varma" ytan till den kallare luften, och därmed transporteras värme bort från isen. Denna borttransport blir effektivare när det blåser. Är emellertid luften varmare än isen tillförs värme också effektivare vid blåst. Eftersom det framför allt är värme från vattnet under isen som ska ledas bort är denna effekt störst då isen är tunn. Större istjocklek innebär bättre isolering av vattnet.
I gränsskiktet ovanför isens yta blir luften fuktig. Om
omgivande luftfuktighet är låg, kommer denna hinna att lättare ledas bort,
varvid det måste komma upp ny ånga ur isen för att uppehålla det fuktiga gränsskiktet.
Ju torrare luften är, desto större blir borttransporten av värme, och isen växer
således snabbare. Viktigt att notera är att isen sublimerar i stor utsträckning.
D.v.s. isen övergår direkt från fast- till gasform. Denna process är mycket
energikrävande och ger alltså en snabb istillväxt.
Även i detta fall spelar vinden stor roll.
Vatten har sin största täthet vid 4°. Det innebär alltså att vattnet är lättare vid både 0° och 15°. På hösten kyls ytvattnet ner och börjar därmed sjunka. Man säger att sjön skiktar sig. Först när sjön skiktats klart kan isläggning påbörjas. Detta förklarar de olika tidpunkterna när sjöar lägger sig. I samband med skiktningen transporteras vattnets värme upp i luften. Ju mer värme som kan transporteras bort från vattnet desto fortare går isbildningen.
Notera att alla formler och grafer är kraftigt förenklade. Det är inte möjligt att med så få parametrar få ett exakt resultat. Dock kan detta ge en grov indikering.
 |
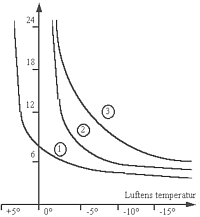Istillväxten varierar mycket beroende på
vind, väder och temperatur.
Grafens Y-axel motsvarar antal timmar per cm bildad is. X-axeln motsvarar lufttemperatur. Ur grafen kan vi ta ett exempel:
|
|
|
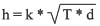
Matematiskt kan istillväxten beräknas enligt formel. Där h är istjocklek, T är dygnsmedeltemperaturen, d är antal dygn och k en faktor. Under gynnsamma förhållanden är k = 2,2. |
|
|
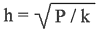
För is som frusit under gynnsamma förhållanden kan nödvändig istjocklek beräknas enligt formel. Där h är istjocklek, P är maxlast och k en faktor. För en skridskoåkare som färdas på hyfsad is är k = 4. Räkneexempel ger då att för en person på 100 kg så ger 5 cm is tillräcklig bärighet. |
Tyvärr inträffar det allt som oftast att det faller snö på den nylagda isen. Många tror att snön nu ligger kvar och att isen inte är gång eller åkbar.
När det blåser eller snöar vid den första isbildningen kommer det tunna isskiktet att få ett annorlunda utseende. I stället för klara skivor bildas isnålar, sönderblåsta ishinnor och snöblandad is. Detta påverkar i sin tur den underliggande kärnisen. Kristallerna blir som smala pinnar (1-10 mm) vilket gör isen segare och mindre känslig för temperaturväxlingar. Snöinblandning i de översta skiktet medför även något långsammare istillväxt.
Fortsatt snöfall leder så småningom till att det flytande istäcket pressas ner i vattnet. Vatten kan då börja strömma upp (t.ex. genom landsprickor) och sprids lätt över ett stort område. Vattnet sugs upp en bit i snön (varierar med snötyp och temperatur) varefter den vattenblandade snön kan börja frysa uppifrån och ner mot den underliggande isen. Den mjölkfärgade istyp som då bildas kallas stöpis. Egenskaperna varierar kraftigt främst beroende på luftinblandningen och storleken på luftbubblorna. Kristallerna är många och små (ca 1 mm) vilket gör isen segare och förhållandevis stark.
Under förutsättning att stöpisen har frusit ordentligt samman med underliggande is bidrar den till en förhöjd bärförmåga. Ofryst snöis blandning kallas stöp. Så länge det finns ofrusen stöp i isen kan det inte ske någon istillväxt under kärnisen.
Då man åker skridskor på tunn blankis kan man höra en sjungande ton från isen. Tonhöjden varierar med isens tjocklek, ju tunnare is desto högre ton -högre frekvens. Vana åkare använder tonhöjden som indikation på istjockleken. Man hör inte tonen så tydligt från sin egen åkning, men starkare från skridskoåkare på avstånd. Kan en person med guldöron direkt höra isens tjocklek? Hur uppkommer tonen?
Akustiker har i urminnes tider teoretiserat över oändligt stora plattor. Teorier för ljudisolering i hus bygger på att man koncentrerar synfältet till en enstaka vägg, och betraktar en väggyta på 3 x 2,5 m som en oändligt stor skiva. Man beräknar egenskaperna för den oändliga skivan, och på slutet lägger man in lite ingenjörsmässiga korrektioner för att väggen trots allt inte är så stor. Tricket innebär stora förenklingar, eftersom man inte behöver ta hänsyn till reflexer och vad som händer vid väggens anslutningar. Man har reducerat modellen till 1 frihetsgrad. Man glömmer de låga frekvenserna och att det finns resonanser i det verkliga livet. Inverkan av resonanser är ju störst vid låga frekvenser. Man sveper med den breda tuschpennan. För att ingen skall begripa något använder man alltid dB.
Vibrationsspecialister däremot bygger sina teorier med punktmassor och ideala fjädrar. Man är specialist på stelkroppsrörelser. Då man måste analysera stora system, t ex en vägg, betraktar man ett hörn med en modell som är sammansatt av många små element. Man drar gärna till med minst 100.000 frihetsgrader och det vill ändå aldrig riktigt räcka till. Stor omsorg läggs på att beskriva vad som händer i modellens kanter. Man älskar resonanser. Man glömmer de höga frekvenserna och att det finns mekaniska förluster i det verkliga livet. Man ritsar med stålstiftet. Man måste alltid inför varje ny beräkning köpa ny dator.
Det ligger nära till hands att betrakta is på en stor sjö som en oändlig skiva - vi kör med akustikperspektivet.
Den hörbara tonen i luften orsakas av vibrationer (böjvågor) i isen som sätter igång en tryckvåg (kompressionsvåg) i luften.
Elementära övervägande medför att normala böjvågsresonanser (stående vågor som orsakar interferens med vågor som reflekteras i isens kanter), kan uteslutas som orsak. Resonansfrekvenser av den typen är omvänt proportionella mot isens dimensioner. Redan för en 1 km lång sjö, skulle resonanser av den typen hamna i milli-Hertz-området. De kan inte uppfattas med hörseln. Man hör frekvenser på ca 20 - 20000 Hz, och bäst vid ca 500- 2000 Hz. Man kan också tänka sig en stående våg mellan isens över- och undersida. Vid istjocklek på ca 100 mm erhålls en resonans på ca 100.000 Hz. Den är inte hörbar för människor.
Nej, det är troligtvis frågan om sk koincidens. Vid en viss frekvens som beror på isens tjocklek erhålls en mycket stark koppling mellan böjvågen i isen och kompressionsvågen i luften. Det är nämligen så att ljudhastigheten i luften är oberoende av frekvensen. Vid skridskotemperaturer (-5 °C) uppgår ljudhastigheten i luft till ca 330 m/s. Böjvågshastigheten i isen däremot beror på frekvensen. Detta innebär också att våglängden i luften och våglängden i isen är olika långa utom vid en viss frekvens, den sk koincidensfrekvensen.
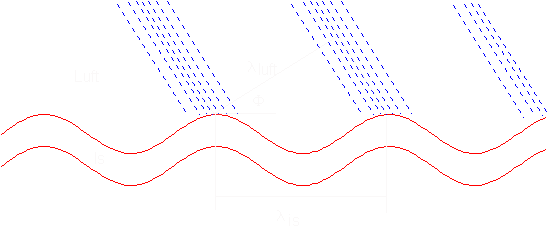
I gränsövergången mellan is och luft gäller: lluft=lis · cos f. Koincidens för f=0.(Våghöjden är kraftigt överdriven, se sid 4.)
Med ett slag i isen eller den lätta impulsen från skridskoåkarens skär exciteras böjvågor i isen med alla frekvenser. Vid låga frekvenser, då våglängden i luft är längre än böjvåglängden i isen, sker ingen ljudutstrålning. Ljudvågen kollapsar hela tiden. Den släcker ut sig själv. Vid koincidensfrekvensen stämmer våglängderna och våghastigheterna exakt. Böjvågen i isen exciterar en kompressionsvåg i luften som stryker längs med isens yta. Man hör tonen på skridskoåkaren bäst då han befinner sig på håll. Vid högre frekvenser sker fortfarande ljudutstrålning, dock inte lika effektivt och dessutom riktas ljudvågen snett uppåt.
För att beräkna böjvåglängd och koincidensfrekvens erfordras uppgifter om isens densitet och elastiska egenskaper. Vattnet på isens undersida medför massbelastning och en ökning av koincidensfrekvensen. Här utförs beräkningar för is med luft på båda sidor. Dock reduceras E-modulen så att beräknad frekvens överenstämmer med uppmätt frekvens (två mätningar). En minskning av E-modulen ger ju också en ökning av koincidensfrekvensen. I litteratur anges E-moduler på 4 -10 GPa. Här används en skenbar E-modul på 2,8 GPa. 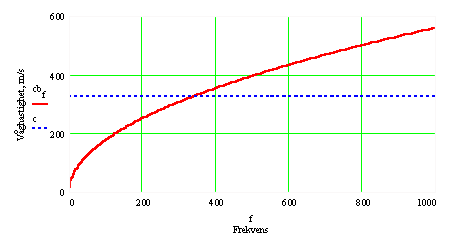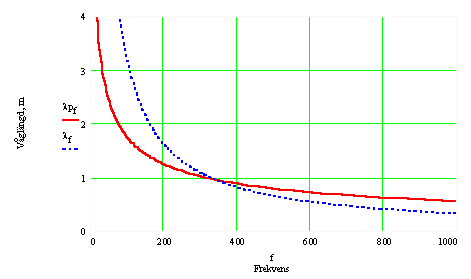Poissons tal = ca 0,3, och Densiteten = ca 990 kg/m3. Nedan redovisas beräknade våghastigheter och våglängder som funktion av frekvensen för en istjockleken 100 mm. heldragen=is;streckad= luft.
Praktiskt användbart blir det först om man beräknar koincidensfrekvensen, dvs frekvensen för den sjungande tonen i isen, som funktion av isens tjocklek.
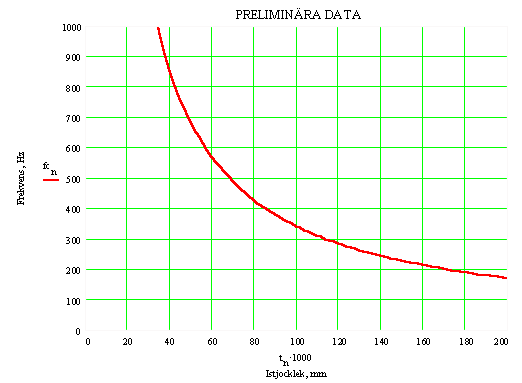
Kärnis på ca 3 cm håller nog för en person på 80 kg om man är otroligt försiktig och villig att chansa lite. Redan vid 6 cm hörs en oroväckande, klagande ton.
För att ta fram säkrare samband mellan tonhöjd och istjocklek erfordras mätningar på olika isar med olika tjocklek. Erfarna skrinnare "kalibrerar" då man börjar åka på tunn is. Förändringar av istjockleken hörs enkelt även av icke-musiker. I praktiken kör man med relativmätning. Den största osäkerheten torde vara att isens E-modul kan variera pga isen karaktär, kärnis, stöpis, våris etc. Snö på isen minskar ljudstyrkan och försvårar bedömningen.
